Introduction
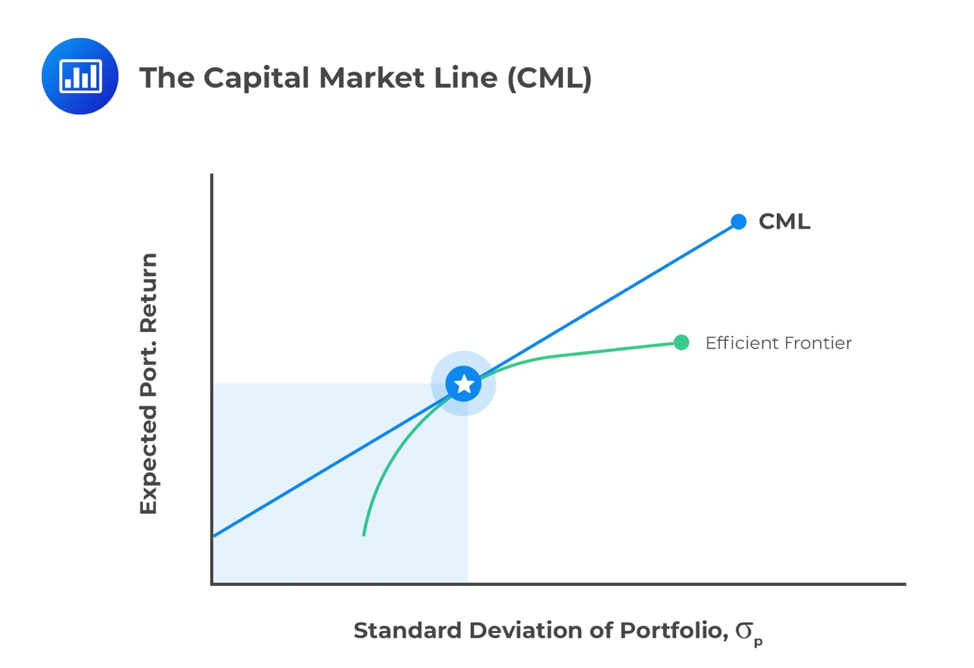
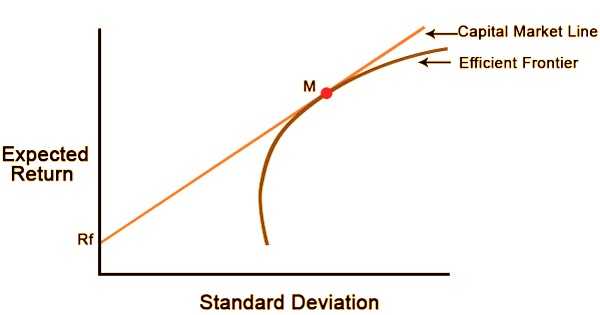
Capital Market Line is a graphical representation of all the portfolios that optimally combine risk and return. Capital Market Line is a theoretical concept that gives optimal combinations of a risk-free asset and the market portfolio.
It’s a tangent line drawn from the risk-free asset’s point to the risky asset’s feasible field. The CML addresses portfolios that ideally join hazard and return; the Capital asset pricing model (CAPM), portrays the compromise among hazard and return for proficient portfolios.
The CML varies from the more famous effective outskirts in that it incorporates hazard free ventures. The capture point of CML and productive boondocks would bring about the most effective portfolio, called the intersection portfolio. With the exception of the Market Portfolio, which is the tangent to the efficient frontier, all points along the CML have superior risk-return profiles to any portfolio on the efficient frontier.
The Capital Market Line (CML) formula can be written as follows:
ERp = Rf + SDp * (ERm – Rf) /SDm
where,
- Expected Return of Portfolio
- Risk-Free Rate
- Standard Deviation of Portfolio
- Expected Return of the Market
- Standard Deviation of Market
All of the portfolios on the CML have the same Sharpe ratio as that of the market portfolio, i.e.
Example:
The risk-free rate is currently 3%, and the expected market return is 15%, with a standard deviation of 7%.
We have two different portfolios with which we can compare: the standard deviation from portfolio A is 4%, while the standard deviation from portfolio B is 9%.
We calculate the expected return on portfolio A as follows:
E (R)A= 3 + 4{(15 – 3)/7}
= 3 + 4 (1.7)
=9.85%
Similarly, we will calculate the expected return of portfolio B as follows:
E (R)B= 3 + 9{(15 – 3)/7}
= 3 +9(1.7)
=18.3%
A stock picking rule of thumb is to buy assets whose Sharpe ratio will be above the CML and sell those whose Sharpe ratio will be below. Indeed, from the efficient market hypothesis it follows that it’s impossible to beat the market. Therefore, all portfolios should have a Sharpe ratio less than or equal to the market’s. In consequence, if there is a portfolio (or asset) whose Sharpe ratio will be bigger than the market’s then this portfolio (or asset) has a higher return per unit of risk, which contradicts the efficient market hypothesis.
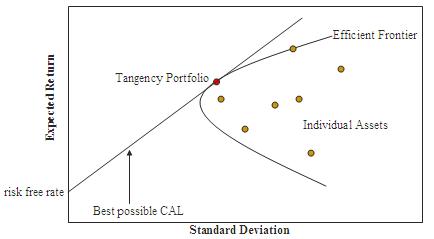
The CML is an uncommon adaptation of the Capital Allocation Line (CAL). The CAL shows a proficient boondocks for an arrangement of hazardous resources. The CML stands for absolute risk, and the SML measures it (beta or systematic risk). Fairly priced securities always plot on the SML and CML.
Investors “POV”
Investors that are risk averse would choose portfolios that are similar to the risk-free asset, choosing low volatility over higher returns. Investors that are less risk averse would favor portfolios that are higher on the CML, with a higher expected return but more volatility. In result, if there is a portfolio (or resource) whose Sharpe proportion will be greater than the market’s then this portfolio (or resource) has a better yield for each unit of hazard, which repudiates the productive market speculation. There are sure suppositions that exist inside the idea of Capital Market Line. In the real world, however, these assumptions are often broken. Markets, for example, are not frictionless. The transactions have certain costs associated with them.
Efficient Frontier
In modern portfolio theory, the efficient frontier (or portfolio frontier) is an investment portfolio which occupies the “efficient” parts of the risk–return spectrum. A combination of assets, i.e. a portfolio, is referred to as “efficient” if it has the best possible expected level of return for its level of risk (which is represented by the standard deviation of the portfolio’s return).
The positively sloped (upward-sloped) top boundary of this region is a portion of a hyperbola and is called the “efficient frontier”.
Assumptions
The portfolios with the best trade-off between expected returns and variance (risk) lie on this line. The tangency point is the optimal portfolio of risky assets, known as the market portfolio. Under the assumptions of mean-variance analysis—that investors seek to maximize their expected return for a given amount of variance risk, and that there is a risk-free rate of return—all investors will select portfolios that lie on the CML.
According to Tobin’s separation theorem, finding the market portfolio and the best combination of that market portfolio and the risk-free asset are separate problems. Individual investors will either hold just the risk-free asset or some combination of the risk-free asset and the market portfolio, depending on their risk-aversion.
Capital Market Line vs. Security Market Line
The CML is sometimes confused with the security market line (SML). The SML is derived from the CML. While the CML shows the rates of return for a specific portfolio, the SML represents the market’s risk and return at a given time, and shows the expected returns of individual assets. And while the measure of risk in the CML is the standard deviation of returns (total risk), the risk measure in the SML is systematic risk or beta.
Securities that are fairly priced will plot on the CML and the SML. Securities that plot above the CML or the SML are generating returns that are too high for the given risk and are underpriced. Securities that plot below CML or the SML are generating returns that are too low for the given risk and are overpriced.
The SML is derived from the CML. While the CML shows the rates of return for a specific portfolio, the SML represents the market’s risk and return at a given time, and shows the expected returns of individual assets. And while the measure of risk in the CML is the standard deviation of returns (total risk), the risk measure in the SML is systematic risk or beta.
Conclusion
The Capital Market Line (CML) draws its basis from the capital market theory and the capital asset pricing model. It is a theoretical representation of different combinations of a risk-free asset and a market portfolio for a given Sharpe Ratio.